Le Traiettorie del Biliardo - pt. 1
Introduzione
E’ un bel po’ di tempo che con la redazione si era deciso di cominciare una sezione sulla tecnica del biliardo. Questa rubrica, dedicata ai sistemi di conteggio, inaugura la nuova iniziativa del Magazine.
L’idea è quella di poter dare ai nostri lettori dei validi spunti per approcciare al meglio il gioco del biliardo, tentando anche l’interpretazione di fenomeni in apparenza di difficile spiegazione.
Prima di iniziare questa avvincente sfida mi preme specificare una cosa molto importante: qualunque sistema che sia numerico o di puro riferimento deve servire esclusivamente ad interpretare le diverse situazioni di gioco. In questo si vuol intendere che un conteggio non deve essere utilizzato esclusivamente per – come si dice in gergo – prendere biglia, ma deve servire per interpretare correttamente il tiro che stiamo andando ad eseguire.
Ritengo questa formulazione importante al fine di non illudere il lettore che imparare un conteggio vuol dire imparare a fare i punti.
Imparare un sistema vuol dire assimilare informazioni utili ai fini del gioco. Personalmente ritengo che saper contare le 3 sponde non significa prendere biglia e fare il castello, ma significa avere nozioni importanti su quale sarà il percorso globale della biglia, con l’obiettivo di poter ricavare sempre la soluzione migliore.
Il nostro scopo sarà quindi quello di ottenere indicazioni sulle traiettorie del biliardo.
Per far questo il modo migliore è innanzitutto l’introduzione di una unità di misura riproducibile su ogni biliardo, un metro di giudizio su cui riferire le nostre ipotesi e tesi.
Esattamente con un falegname utilizza il metro noi sul biliardo utilizzeremo i diamanti. Nonostante questi siano disegnati ad una distanza convenzionale di 35,5cm l’uno dall’altro, per comodità noi ragioneremo in ordine di punto-diamante.
Per punto s’intende 1/10 di diamante, che in termini di lunghezza equivarrebbe a 3,55cm (circa due dita di una mano). Da questo risulta evidente quanto un sistema di conteggio può diventare approssimativo considerando che il diametro di una biglia vale poco più di 6cm. Quindi se da un lato questa osservazione schernisce l’utilità immediata di un conteggio, dall’altro spinge il ricercatore a formularne sempre di più precisi. Nonostante questa incessante ricerca possiamo evitare di commettere l’errore che molti in passato hanno perpetrato, dichiarando fin d’ora che nessun conteggio ci consentirà mai di raggiungere la perfezione assoluta, altro non fosse che oltre a consueti errori di valutazione, un giocatore può commettere errori di applicazione, generalmente ancor più determinanti.
A questo punto sarebbe opportuno aprire una parentesi sulle potenzialità di applicazione, ossia quanto possa essere ad esempio utile saper contare una candela se poi al momento del tiro vizio la battente con dell’effetto. Infatti a differenza del gioco ad occhio, in cui ognuno personalizza le proprie esecuzioni riuscendo a quantificare e compensare i propri difetti, magari inconsciamente, quando ci si affida a sistemi di conteggio, che per definizione sono oggettivi, vengono messe in risalto tutte una serie di lacune da parte del giocatore. In questo l’utilità di un sistema di conteggio è quella di far rendere conto a colui che lo applica quali siano i limiti d’impostazione, di sensibilità, ecc… contribuendo in maniera positiva alla crescita del giocatore. Poiché questo campo esula dalla trattazione di questa rubrica, daremo sempre per scontato la vostra abilità in fase di mira e di punteria.
La Geometria
Cominciamo quindi la nostra trattazione dalle origini: la geometria.
Poiché le sponde del biliardo sono elastiche in linea di principio riflettono le diagonali di incidenza con delle traiettorie di riflessione, proprio come uno specchio rifletterebbe un fascio di luce. Se una biglia fosse un punto materiale e non avesse rotazione scivolando senza attrito sul panno e sulle sponde determinerebbe delle traiettorie in uscita esattamente tali e quali a quelle di entrata, stabilendo così un principio della fisica ottica, criterio che per comodità sul biliardo prende il nome di teoria del triangolo isoscele.
Per definizione l’altezza di un triangolo isoscele è anche la bisettrice dell’angolo tra i due lati uguali. Pertanto (con l’altezza perpendicolare al punto d’impatto su sponda) potremmo identificare in questi due lati le traiettorie di entrata e di uscita di una biglia a sponda. Conoscendo il punto di partenza e quello di arrivo, ossia i vertici della base del triangolo isoscele, potremmo ricavare lo scostamento del vertice alto del triangolo rispetto al punto di partenza, dividendo per 2 la base. Se ad esempio partissimo da un angolo del biliardo, per raggiungere l’altro angolo adiacente dovremmo indirizzare la biglia verso il punto mediano della sponda lunga di mira. In questo caso i due angoli si identificano con i vertici della base, mentre il punto di mira con il vertice dell’altezza.
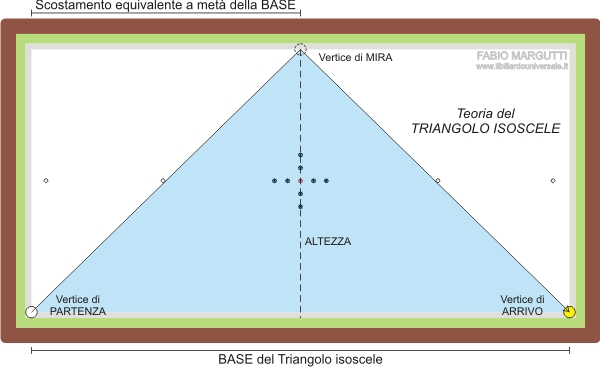
Nella figura sotto sono riportati alcuni triangoli isosceli che determinano traiettorie per raggiungere sempre lo stesso angolo.
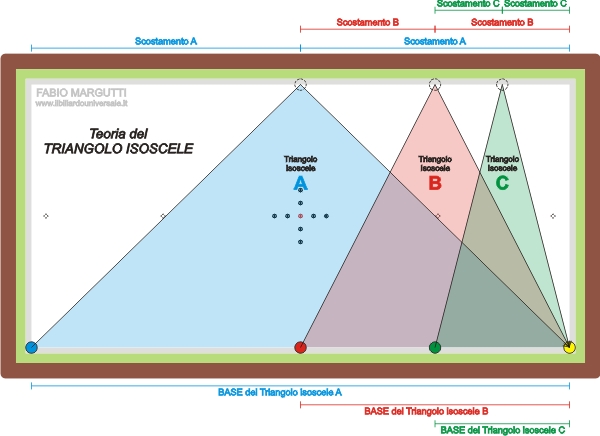
Finora abbiamo per comodità affrontato l’arrivo sempre nel solito angolo ma il metodo può essere applicato in qualunque posizione del biliardo. Basta conoscere l’ampiezza della base e dividerla per due per ottenere lo scostamento del punto di mira. E’ implicito che tale scostamento può essere:
1) aggiunto al vertice di partenza,
oppure
2) sottratto al vertice di arrivo.
La scelta del procedimento da applicare è del tutto soggettiva poiché ai fini teorici il punto di mira ricavato è perfettamente equivalente. (Il mio consiglio è comunque quello di usare la seconda strada, ossia di sottrarre lo scostamento al punto di arrivo. E’ ancora troppo presto per spiegarne il motivo, ma tra qualche tempo capirete da soli il vantaggio di tale scelta)
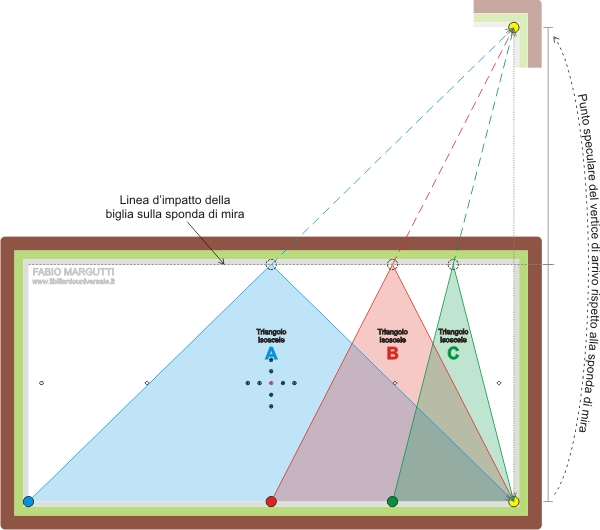
A questo punto se osserviamo bene le traiettorie in entrata possiamo notare che queste hanno in comune qualcosa di determinante. Prolungandole fuori dal biliardo s’intersecano in un punto ben preciso che per geometria è perfettamente speculare all’angolo (vertice) di arrivo rispetto alla linea d’impatto della biglia lungo la sponda di mira.
Anche se piuttosto banale, questo risultato evidenzia un concetto piuttosto importante: le traiettorie sul biliardo vanno cercate fuori dal biliardo.
Infatti partendo da qualunque posizione del biliardo e mirando sempre nello stesso punto esterno al biliardo otterrei, specularmente rispetto al punto d’impatto, sempre lo stesso arrivo geometrico.
Quando si racconta di giocatori che per eseguire un tiro diretto o indiretto mirano un gessetto fuori dal biliardo oppure un segno sul muro – o addirittura la stecca del compagno che si posiziona in direzione per dare il giusto riferimento – ci si riferisce proprio a questo metodo.
Nelle prossime lezioni
Per rendere questo metodo applicabile su qualunque biliardo, al fine di non dover ricorrere continuamente a riferimenti esterni, tenteremo di attribuire una particolare numerazione alle losanghe disegnate lungo le sponde.
Una volta determinata tale numerazione cercheremo di capire in che maniera la componente fisica influenza particolarmente tali soluzioni geometriche, e come può essere brillantemente consolidato il binomio geometria-fisica del biliardo.