Le Traiettorie del Biliardo - pt. 2
La Fisica
Nella precedente lezione introduttiva abbiamo cominciato ad osservare le traiettorie nel biliardo attraverso un riferimento esterno al piano di gioco che abbiamo definito punto speculare dell’angolo di arrivo. Mirando da qualunque posizione questo punto virtuale otterremo una risultante diagonale geometrica che conduce esattamente nell’angolo (o buca) di arrivo.
Purtroppo e per fortuna la realtà del gioco del biliardo si discosta sostanzialmente da un sistema così statico: purtroppo perché implementa le difficoltà di chi tenta di costruire dei sistemi analitici, per fortuna perché permette a questa splendida disciplina di essere così tanto affascinante.
Sinceramente io preferisco di gran lunga il per fortuna ma vi confesso che a volte nei momenti di smarrimento di gioco cedo debolmente al purtroppo.
I purtroppo ed i per fortuna nel loro insieme racchiudono tutti quei fenomeni fisici che alterano, più o meno, la pura geometria.
Ricordiamo che le biglie sul tavolo possono saltare, slittare, curvare o andare dritte (quest’ultima di solito la situazione meno realistica). Questo perché in quanto oggetti sono innanzitutto soggette alle leggi naturali, e quindi essendo sferiche ruotano, essendo elastiche rimbalzano, essendo pesanti saltano, slittano, si muovono e poi si fermano.
In questo percorso ideale la biglia cambia costantemente la sua rotazione ed il suo stato di moto, influenzata soprattutto dalle condizioni ambientali (temperatura ed umidità), dalle condizioni di usura del piano di gioco, dalle sponde, ecc…
Alla luce di quanto esposto risulta evidente che non esiste un criterio infallibile di calcolare il biliardo. Così, rubando un concetto alla fisica quantistica (a cui siamo lungi dall’accostarci), il biliardo può essere previsto solamente rimanendo in un certo intervallo di errore. La cosa migliore che si possa fare è assottigliare il più possibile questa legittima approssimazione.
Cerchiamo pertanto di capire come la fisica possa influire determinando le reali traiettorie.
A tal riguardo il nostro approccio sarà quello di osservare il comportamento della biglia battente rispetto a quello puramente geometrico e di dare una spiegazione razionale e logica a quei fattori che possono contribuire alle evidenti divergenze, in maniera più o meno rilevante.
Ipotizziamo di eseguire il colpo su tre diverse tipologie di biliardo, riferendo tale classificazione in relazione al grado di usura del panno:
- Biliardo Nuovo (o con caratteristiche tali),
- Biliardo Semi-Nuovo (o Semi-Battuto),
- Biliardo Battuto.
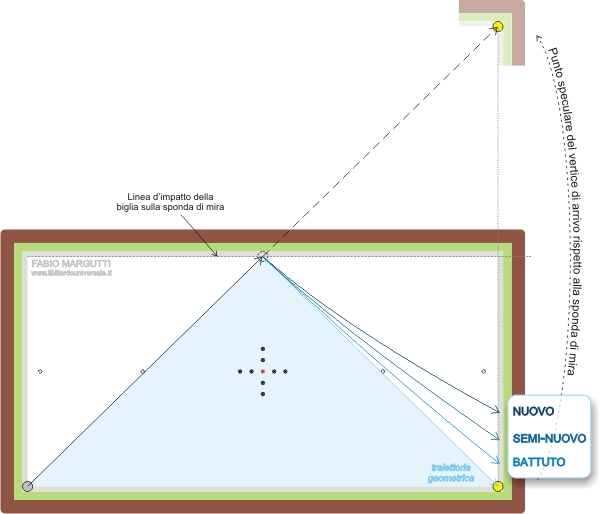
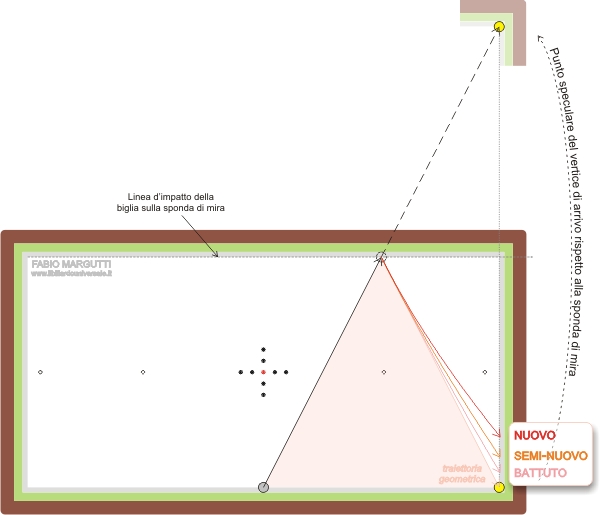
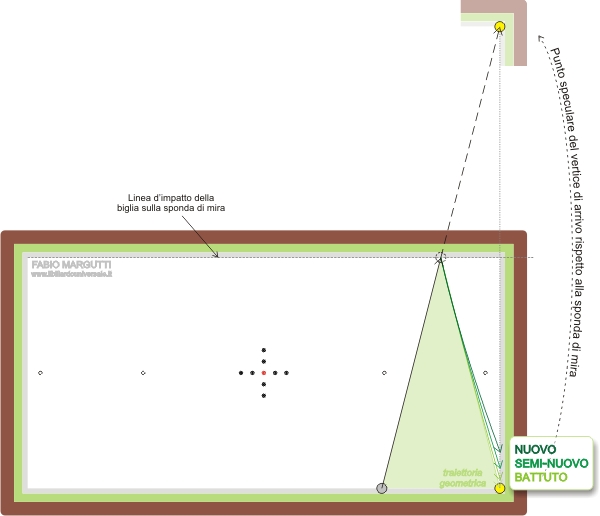
Queste figure si riferiscono ad un’esecuzione di forza moderata quando cioè la biglia battente prima d’impattare la sponda di mira rotola passivamente sul tavolo di gioco, priva di ogni forma di rotazione laterale o verticale, completando un percorso di circa 7 metri (in gergo equivalente ad una passata e mezzo, scarsa).
Come è facilmente evidenziabile la traiettoria della biglia subisce una deviazione importante a seguito dell’impatto contro sponda, differente per ogni tipologia di biliardo.
In sostanza, mentre la geometria restituisce semplicemente una traiettoria speculare, la fisica di ogni biliardo restituisce:
1) una direzione,
2) una condizione di moto,
3) una rotazione.
Dalla combinazione di queste tre componenti si genera ogni traiettoria sul biliardo. Generalmente questa traiettoria non ha un andamento rettilineo ma è piuttosto curvilinea, con una concavità/convessità che si accentua a seconda:
- dell’angolo d’incidenza,
- della forza del tiro,
- della rotazione e dello stato di moto della biglia al momento e successivamente al contatto su sponda,
- e per tutta una serie di condizioni secondarie, ma non meno importanti, tipo la temperatura del piano di gioco, il tasso di umidità ambientale, la pulizia, ecc…
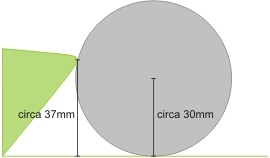
Nei casi sopra esposti la sponda si contrappone al moto della biglia, consentendole di cambiare direzione di corsa. Poiché la sponda presenta in sezione mediale una geometria triangolare, con il vertice rivolto al piano di gioco più alto rispetto al raggio della biglia, determina in primis l’insaccamento della biglia nella sponda stessa. Il ritorno elastico di questo insaccamento genera una controspinta grosso modo uguale e contraria alla spinta in entrata. In effetti la spinta iniziale non è del tutto recuperata perché viene in parte convertita in effetto naturale di sponda (e ad essere precisi un’altra discreta parte viene persa sotto forma di calore e per la non perfetta elasticità del sistema panno-sponda).
In sostanza quindi la sponda non può essere considerata un vero e proprio specchio geometrico, ma un ostacolo fisico non perfettamente definibile.
Come se non bastasse la direzione che la biglia acquista dopo l’urto su sponda è solo uno dei fattori che influenzano la traiettoria macroscopica risultante. Infatti subito dopo il contatto su sponda segue un breve tragitto in cui la biglia plana sul panno, slittandovi sopra.
Al termine di questo frangente la biglia passa dalla direzione impartitale dalla sponda verso una nuova direzione derivante dalla propria rotazione (rispetto alla nuova direzione). Tutto questo si traduce con il fenomeno che in gergo prende il nome di scivolamento.
Quando si dice che la sponda del biliardo nuovo fa scivolare la biglia in realtà è un luogo comune riduttivo, perché gran parte del merito di questo fenomeno è attribuibile anche al piano di gioco.
Nelle prossime lezioni
In questa lezione abbiamo incominciato a prendere dimestichezza con un po’ di fisica del biliardo.
Anche se parecchi degli elementi fin qui incontrati sembrino giocare a sfavore di un sistema generale scopriremo come e perché il sistema dei centri virtuali supera tali difficoltà, abbracciando la fisica e la geometria del biliardo. Applicheremo per la prima volta gli effetti per stabilizzare le traiettorie.