Le Traiettorie del Biliardo - pt. 18
Questa lezione completa il secondo anno di questa rubrica di tecnica.
Con l’occasione è d’obbligo fare il punto della situazione confrontando ed integrando tra loro le applicazioni algebrico-numeriche del Sistema Margutti fin qui introdotte.
Lo scopo sarà quello di fornire dei riferimenti utili quando ci troviamo ad eseguire dei tiri con partenza dalla sponda corta, quali: 3sponde (o più), garuffe, strisci, ecc…
ripasso del sistema margutti
Abbiamo detto che ogni arrivo del biliardo è rappresentato ed individuato in un centro virtuale fuori dal biliardo, un CentroMultiplo (CM) fisico. Mirando il relativo CM, con la stessa forza, sbracciata e taglio, la biglia eseguirà un percorso all’interno del rettangolo di gioco e terminerà la sua corsa sul medesimo arrivo, che sia esso lungo una sponda o in mezzo al biliardo.
Poiché ogni punto esterno al biliardo può essere considerato un CM, spinti dalla necessità di dettare un po’ di ordine in questo immenso spazio, abbiamo inizialmente individuato un asse lungo il quale sono disposti una serie di centri di convergenza, che mirati con determinati effetti permettono di ottenere dei comuni arrivi del gioco all’italiana.
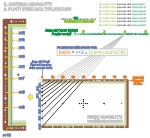 Fig. 1:
Fig. 1:
Una delle applicazioni a Punti Fissi Moltiplicatori del Sistema Margutti. I PF Moltiplicatori si trovano sul margine tra la sponda ed il panno e vanno memorizzati così come vengono propostiChiaramente questa distribuzione geografica dei CM varia da biliardo a biliardo, e può essere utilizzata come termine di paragone per confrontare due tipi differenti di biliardo, da qui la definizione di impronta digitale propria di ogni biliardo.
Quando ad esempio diciamo che il tiro di striscio stringe su un tavolo rispetto ad un altro, vuol dire che la fisica e la geometria globale di quel tiro su un biliardo viene espressa da un CM mentre su un altro biliardo può essere codificata da un CM leggermente più spostato. Da qui otteniamo diagonali più aperte e diagonali più chiuse.
Chiaramente ogni singolo spostamento della generica distribuzione ideale di CM comporta la deformazione globale di tutta la regione. Infatti laddove lo striscio chiude si presuppone che anche i CM di altri tiri strettamente imparentati (come la mezza garuffa) si spostino di conseguenza.
In tal modo da una singola prova si ottengono informazioni preziose per interpretare anche altre esecuzioni.
Se prima vi dovevate adeguare ad un biliardo attraverso le compensazioni, con questo nuovo approccio imparerete a ragionare su un biliardo per le sue caratteristiche, e quindi per come è.
Infatti è improprio dire che un biliardo stringe o allarga di tot punti, ma è più idoneo parlare di caratteristiche, di misurazioni oggettive.
Troppo spesso si sente raccontare di biliardi che allargano di tot punti quando sarebbe più naturale dire che il CM di quel tiro su quel biliardo si trova lì, in un preciso punto.
Inoltre, sempre nella valutazione del sistema, va menzionato che uno stesso CM può essere sfruttato anche per arrivi differenti. Ad esempio un CM può essere utilizzato genericamente per arrivare su un punto della 3a sponda (sul panno) quando viene dosato un determinato effetto buono, oppure può essere ricercato per giocare una garuffa di effetto a reggere o per uno striscio di battuta.
SM mnemonico e a PuntiFissi
In definitiva una buona chiave di lettura di un biliardo è saper analizzare i suoi CM fisici, ossia i centri di convergenza che occorre mirare per ottenere determinati arrivi.
A tale proposito abbiamo introdotto diverse applicazioni o metodi per essere in grado, giocando, di ricondurre le diverse traiettorie verso il relativo Centro Multiplo.
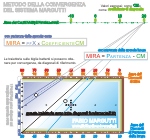 Fig. 2:
Fig. 2:
Il metodo della convergenza: per ottenere una specifica diagonale sulla biglia battente è consigliabile convergere tra due diagonali simili, vicinePoiché queste applicazioni algebrico-numeriche sono state già esposte nelle precedenti lezioni qui ne riporto solo una rappresentazione grafica a testimonianza della loro integrazione.
Chiaramente useremo le due applicazioni finora introdotte, quindi l’SM Mnemonico e l’SM a Punti Fissi Moltiplicatori per le partenze dalla sponda corta, ed il classico metodo delle differenze per le partenze dalla sponda lunga.
Abbiamo inoltre spiegato che un’applicazione deve servire ad applicare praticamente il sistema di riferimento, quindi nel nostro caso il Sistema Margutti. Poiché esso si basa sul principio di convergenza verso un determinato CentroMultiplo, possiamo rendere elastico e malleabile ogni tipo di applicazione in quanto per ottenere una qualunque diagonale basterà ricavarla grazie al metodo della convergenza (spiegato nella precedente lezione) da una diagonale conosciuta di riferimento.
In sostanza i numeri che usiamo non sono più sterili attribuzioni privi di significato logico, ma servono a tradurre una vera e propria unità di misura, quella spaziale dei CM fisici fondamentali.
In questo modo qualora si voglia ottenere una diagonale particolare, non servirà più contarla.
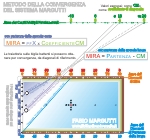 Fig. 3:
Fig. 3:
Metodo della convergenza del Sistema Margutti. Per ottenere una diagonale particolare basta usare una diagonale basilare (o conosciuta) ed il buon sensoSe ad esempio volessi determinare una diagonale18 basterà cercare la diagonale20 con l’SM a Punti Fissi Moltiplicatori e chiudere leggermente la traiettoria.
Allo stesso modo qualora volessi ottenere una diagonale10 dal primo diamante della sponda corta basterà ricordare, tramite l’SM Mnemonico, che diamante-diamante equivale ad una diagonale8; e quindi che la diagonale10 potrà essere ottenuta aprendo di qualche punto questa traiettoria di riferimento.
significato algebrico dei pf
A tal riguardo ci vengono in aiuto i famosi Punti Fissi (o PF).
I PF sono molto importanti anche perché indicano quanto vale un punto-diagonale da quella partenza. Ad esempio qualora mi trovassi nell’area di un PF7 saprei che ogni punto-diagonale vale 0,7punti di sponda di mira. Nella zona del PF5 ogni punto-diagonale vale 0,5punti.
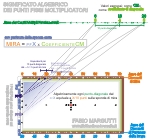 Fig. 4:
Fig. 4:
Significato geometrico/matematico dei Punti Fissi Moltiplicatori del Sistema Margutti. Salendo lungo la sponda corta di partenza, l'unità equivalente della diagonale decresce esponenzialmenteSe ad esempio mi trovassi dalla partenza PF6 e volessi trovare una diagonale22 basterebbe cercare la diagonale20 (PF6 x 5 = 30) ed aggiungere 2punti-equivalenti, ossia 0,6 + 0,6 = (circa) 1 punto. Quindi la diagonale22 dal PF6 mira al diamante (PF6 x 5) + 1 = 31.
Chiaramente ora si può anche intuire perché più le partenze sono alte e maggiori sono le difficoltà di eseguire un tiro.
Infatti dal PF3 ogni punto-diamante equivale a 0,3 , ossia in ogni punto di mira ci sono 3punti di diagonale. Si intuisce quindi quanto sia difficile ottenere la giusta mira, e quanto un leggero difetto di esecuzione accentui maggiormente l’errore.
Algebricamente il PFx esprime quanti punti di mira occorre accumulare per aumentare di 10unità una diagonale.
Quindi dal PF10 le diagonali vanno di 10 in 10, dal PF9 di 9 in 9, dal PF8 di 8 in 8, ecc… Ad esempio dal PF5 le decine di diagonale vanno di 5 in 5, e poiché la diagonale0 parte dal 15, la diagonale20 mira il 20, la diagonale30 mira il 25, ecc…
Lo scopo finale di questa rubrica di tecnica sarà quello di proporre un sistema universale non numerico, che permetterà di abbandonare ogni tipo di numerazione ed operazione algebrica a favore di due passaggi visivi, dove per qualsiasi esecuzione basterà conoscere una diagonale di riferimento e la relativa percentuale di convergenza.
Già pubblicato in anteprima nell’Ottobre del 2007 sul mio sito internet www.ilbiliardouniversale.it , questa mia recente applicazione del Sistema Margutti prende il nome di Sistema Margutti Geometrico, o SMG. In pratica tutte le traiettorie del biliardo senza più i numeri…
Nelle prossime lezioni
Determineremo le prime correlazioni tra CM fisico ed Arrivo, relativamente al tipo di trattamento impartito alla biglia battente.